

Una proposición de tipo condicional es falsa únicamente cuando el antecedente es verdadero y el consecuente falso. Cualquier otra combinación de valores de verdad da como resultado una proposición compuesta verdadera.



Veamos ahora la construcción de la tabla de verdad del condicional

Pongamos como ejemplo la proposición compuesta:
“Si haces la tarea entonces obtendrás una calificación alta”
Determino cuántas proposiciones simples tengo:
Observo que tengo dos:
Recordemos que por cuestiones de estilo muchas veces no menciono explícitamente el sujeto, pero lo puedo determinar por la conjugación del verbo.
Sustituyo cada proposición con una letra:
Simbolizo la proposición:
p ⊃ q
Para poder dibujar una tabla en la que quedaran escritas las proposiciones en la parte superior y los valores de verdad que asumen las mismas justo debajo de ellas, se necesita aplicar la siguiente fórmula para saber cuántas posibles combinaciones de verdad tiene mi proposición compuesta:
2n
Donde 2 se refiere a los valores de verdad que puede asumir una proposición (que dentro de esta Lógica sólo son dos: verdadero o falso) y “n” se refiere al número de proposiciones simples que conforman la proposición de la que queremos construir la tabla.
En el ejemplo tenemos:
Donde 2 significa los valores de verdad: verdadero y falso y 2 el número de proposiciones simples
Realizo la operación que me da como resultado 4:
22 = 2 x 2 = 4
Con ello sé que mi tabla tendrá cuatro filas o renglones:
Ahora puedo dibujar la tabla:
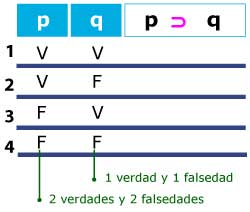
Para asignar los valores de verdad de las proposiciones simples escribo los valores de derecha a izquierda y anoto una V (de verdadero) y una F (de falso). En la siguiente columna duplico el número de verdades y de falsedades. Si hubiera una tercera proposición simple sigo duplicando, es decir, tendría cuatro verdades y cuatro falsedades y así sucesivamente.
Con esta operación obtengo:
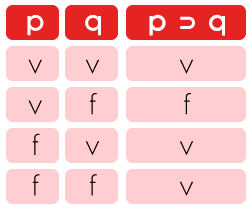
Realiza la tabla de la proposición compuesta p ⊃ q.
En una proposición cuya conectiva lógica principal es el condicional, el miembro que aparece antes de dicha conectiva recibe el nombre de antecedente y el que aparece después de él se llama consecuente.
Una proposición de tipo condicional es falsa únicamente cuando el antecedente es verdadero y el consecuente falso. Cualquier otra combinación de valores de verdad da como resultado una proposición compuesta verdadera.
Siguiendo con el ejemplo del inicio tenemos:
De esta forma tenemos la siguiente tabla:
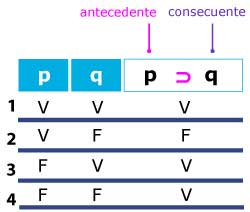
Como puedes notar sólo hay un caso de falsedad que es cuando tenemos el antecedente verdadero y el consecuente falso.
Finalmente veamos la construcción de la última tabla de verdad, la del bicondicional.
Pongamos como ejemplo la proposición:
“Los artículos pueden ser devueltos si y sólo si tienen defectos de fabricación”

Determino cuántas proposiciones simples tengo:
Observo que tengo dos:
Recordemos que por cuestiones de estilo no repito el sujeto, pero sé que me refiero al mismo sujeto (los artículos en este caso) en ambas oraciones.
Sustituyo cada proposición con una letra:
Simbolizo la proposición:
p ≡ q
Para poder dibujar una tabla en la que quedaran escritas las proposiciones en la parte superior y los valores de verdad que asumen las mismas justo debajo de ellas, se necesita aplicar la siguiente fórmula para saber cuántas posibles combinaciones de verdad tiene mi proposición compuesta.
(verdadero y falso) = 2n (No. de proposiciones)
Donde 2 se refiere a los valores de verdad que puede asumir una proposición (que dentro de esta Lógica sólo son dos: verdadero o falso) y “n” se refiere al número de proposiciones simples que conforman la proposición de la que queremos construir la tabla.
En el ejemplo tenemos:
22
Donde 2 significa los valores de verdad: verdadero y falso y 2 el número de proposiciones simples.
Realizo la operación que me da como resultado 4:
22 = 2 x 2 = 4
Con ello sé que mi tabla tendrá cuatro filas o renglones:
Ahora puedo dibujar la tabla:
Para asignar los valores de verdad de las proposiciones simples escribo los valores de derecha a izquierda y anoto una V (de verdadero) y una F (de falso). En la siguiente columna duplico el número de verdades y de falsedades. Si hubiera una tercera proposición simple sigo duplicando, es decir, tendría cuatro verdades y cuatro falsedades y así sucesivamente.
Con esta operación obtengo:
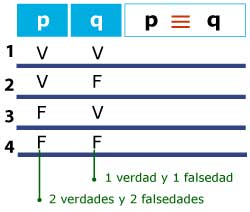
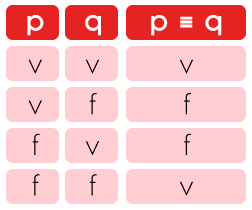
Realiza la tabla de la proposición compuesta p ≡ q.
¿Cuándo es verdadera una proposición compuesta que tiene un bicondicional como su conectiva lógica?
De esta forma tenemos la siguiente tabla:
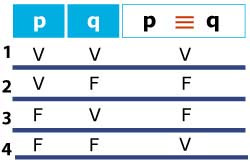
Como puedes observar, cuando las proposiciones simples de una proposición compuesta, cuya conectiva lógica principal es el bicondicional, tienen el mismo valor de verdad, toda la proposición es verdadera. Esto es, si las proposiciones que la componen son ambas verdaderas o ambas falsas, toda la proposición compuesta será verdadera. En cambio, si las proposiciones que la integran tienen valores de verdad contarios, ya sea verdadero y falso o falso y verdadero, entonces toda la proposición compuesta será falsa.

Bien, hemos visto cómo se desarrollan las tablas de verdad con proposiciones simples a partir de las diferentes conectivas lógicas. Ahora, observa los siguientes videos y pon atención, ya que te permitirán lograr una mayor comprensión sobre esta metodología de trabajo.
PaoDacapo (2011, Junio 15) Tablas de verdad. Desarrollo a partir de las conectivas lógicas 1. (Archivo de Video) Recuperado de:http://www.youtube.com/watch?v=HCMM5PiViNc
PaoDacapo (2011, Junio 15) Tablas de verdad. Desarrollo a partir de las conectivas lógicas. (Archivo de Video) Recuperado de: http://www.youtube.com/watch?v=wdsCBSM7ef0

En esta actividad debes colocar las tablas según el lugar que corresponda.

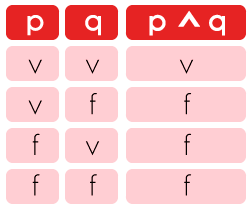
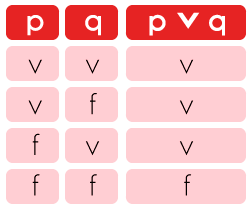
Respuestas:

Escribe debajo de cada proposición simple una V si la proposición es verdadera y una F si la proposición es falsa. Después elabora “la tabla de verdad” para determinar “el valor de verdad” de la proposición compuesta. Da clic en comparar y ve si tu respuesta fue la correcta.

| p |  |
q |
|---|---|---|
Tabla de verdad
| p | q |  |
|
|---|---|---|---|
| 1 | v | v | |
| 2 | v | f | |
| 3 | f | v | |
| 4 | f | f |

| p | v | q |
|---|---|---|
Tabla de verdad
| p | q | p v q | |
|---|---|---|---|
| 1 | v | v | |
| 2 | v | f | |
| 3 | f | v | |
| 4 | f | f |
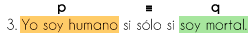
| p |  |
q |
|---|---|---|
Tabla de verdad
| p | q |  |
|
|---|---|---|---|
| 1 | v | v | |
| 2 | v | f | |
| 3 | f | v | |
| 4 | f | f |

| p |  |
q |
|---|---|---|
Tabla de verdad
| p | q |  |
|
|---|---|---|---|
| 1 | v | v | |
| 2 | v | f | |
| 3 | f | v | |
| 4 | f | f |

| ~ | p |
|---|---|
Tabla de verdad
| p | ~ p | |
|---|---|---|
| v | ||
| f | ||

a) Descarga el documento “Tabla de verdad y ciencia” para poder realizar la actividad. play_for_workTabla de Verdad
b) Con base en la información que se te proporciona en el texto, en un documento redacta seis enunciados con la conectiva de la condicional o la bicondicional.
c) Simbolízalos y construye una tabla de verdad de cada uno de ellos. Para construir de manera adecuada la tabla de verdad sigue los cinco pasos que se mencionan en la plataforma.
d) Analiza los resultados de la tabla y redacta una conclusión que puedes inferir a partir de dicha información. ¿La información que puedes inferir de los resultados de la tabla coincide con la presentada en el texto? Si no ¿Por qué? Después revisa tu actividad con la rúbrica. gradeRúbrica